Mat Lab Dot Product Of Two Vectors

The dot product or scalar product of two vectors is used among other things as a way of finding the angle theta between two vectors.

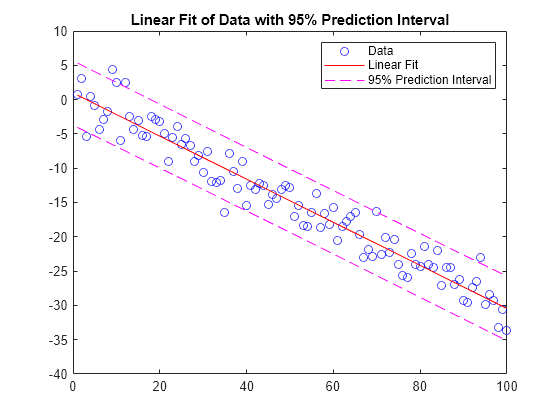
Mat lab dot product of two vectors. This relation is commutative for real vectors such that dot u v equals dot v u. Dot product in this activity you will utilize matlab to evaluate the dot product of two vectors in two different ways using the dot command and using matrix multiplication. Dot product of two vectors a a1 a2 an and b b1 b2 bn is given by a b ai bi dot product of two vectors a and b is calculated using the dot function. The scalar dot product of two real vectors of length n is equal to u v i 1 n u i v i u 1 v 1 u 2 v 2.

A vector is an ordered n tuple which may be represented as a matrix in the form of a column vector nxi matrix or a row vector 1x matrix. Recall that given vectors a and b in space the dot product is defined as. In matlab the appropriate built in function to determine the inner product is dot u v. We can conclude that if the inner product of two vectors is zero the vectors are orthogonal.

B a b cos theta we will use this formula later to find the angle theta. U n v n. The scalar output y is equal to the matlab operation y sum conj u1 u2 where u1 and u2 represent the input vectors.