Mat Lab Dot Product Of Two Vectors By Hand

Use this formula to write a function file which computes the dot product of two 3 dimensional vectors a and b.

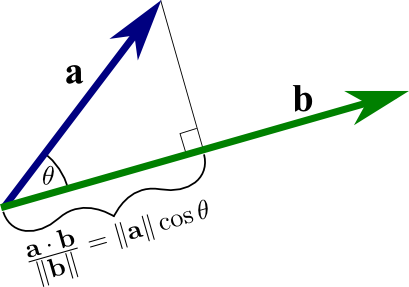
Mat lab dot product of two vectors by hand. The scalar dot product of two real vectors of length n is equal to u v i 1 n u i v i u 1 v 1 u 2 v 2. If a and b are matrices or multidimensional arrays then they must have the same size. The vectors a and b which should contain 3 elements each. This relation is commutative for real vectors such that dot u v equals dot v u.

Here are two vectors. The function calculates the dot product of corresponding vectors along the first array dimension whose size does not equal 1. The cross product a b is defined as a vector c that is perpendicular orthogonal to both a and b with a direction given by the right hand rule. In physics the notation a b is sometimes used though this is avoided in mathematics to avoid confusion with the exterior product.

Cross product is defined as the quantity where if we multiply both the vectors x and y the resultant is a vector z and it is perpendicular to both the vectors which are defined by any right hand rule method and the magnitude is defined as the parallelogram area and is given by in which respective vector spans. The function calculates the cross product of corresponding vectors along the first array dimension whose size equals 3. U n v n. Running the following code.

The function name is dotprod which has two inputs. If a and b are matrices or multidimensional arrays then they must have the same size. A b this means the dot product of a and b. In this case the cross function treats a and b as collections of three element vectors.

The dot product of two column vectors is the matrix product where is the row vector obtained by transposing and the resulting 1 1 matrix is identified with its unique entry. The dot product is written using a central dot. They can be multiplied using the dot product also see cross product. The problem is that in matlab a cross product isn t possible with 2 element vectors.

If a and b are vectors then they must have the same length. If the dot product is equal to zero then u and v are perpendicular. If a and b are vectors then they must have a length of 3. Where the numerator is the cross product between the two coordinate pairs and the denominator is the dot product.

We can calculate the dot product of two vectors this way. In this case the dot function treats a and b as collections of vectors. More generally any bilinear form over a vector space of finite dimension may be expressed as a matrix product and any inner. The output is the single value y which is a.